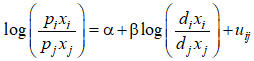von Georg Quaas

Nils Fröhlich und Fabian Richter (2018) plädieren für die Anwendung der Dimensionsanalyse (DA) in der Ökonomik. Obwohl ihr Artikel in einer Festschrift enthalten ist, für die sich wohl nicht jeder interessieren wird, sollte dieses Plädoyer nicht unbeachtet bleiben. Im Vergleich zum Signifikanzproblem stellt es eines der mehr elementaren, aber darum nicht weniger wichtigen messtheoretischen Probleme der theoretischen Verarbeitung von Resultaten empirischer Forschung dar. Unter dem DA verstehen die Autoren die Beachtung der Maßeinheiten, mit deren Hilfe ökonomische Größen gemessen werden. Insbesondere muss die sich auf der linken Seite einer Gleichung ergebende Maßeinheit dieselbe sein wie die auf der rechten Seite. Die Dimensionsanalyse umfasst allerdings mehr als die Überprüfung von Maßeinheiten. Um ein einfaches Beispiel zu nennen: (i) Die Werte von handelbaren Gütern werden üblicherweise in Preisen angegeben, wobei Preise den Wert der Gütereinheit darstellen, also die Dimension Wert je (bestimmter) Gütereinheit haben. Dagegen werden Mengen entweder (ii) in ihren „natürlichen“ Einheiten oder (iii) in deflationierten Werten dargestellt. Ein Vergleich zeigt, dass die Beachtung der Maßeinheiten allein nicht ausreicht, um die formale Korrektheit von Gleichungen abzusichern: Nominale Wertangaben (i) können dieselbe Einheit wie reale Wertangaben (iii) haben, sollten aber trotzdem nicht gleichgesetzt werden. Vielmehr ist es so, dass in den neuen, ab 2005 gültigen Volkswirtschaftlichen Gesamtrechnungen jedes Aggregat mindestens in acht verschiedenen Dimensionen dargestellt werden kann (Quaas 2010: 37). Was man aufgrund der bloßen Unterschiedlichkeiten der Maßeinheiten nicht gleichsetzen kann, wären beispielsweise Wertangaben in Preisen und natürliche Mengenangaben – wie zum Beispiel: 100 Euro = 1 Tonne Äpfel.

Die Beachtung der Maßeinheiten ist also nur eine sehr grobe Methode, um die formale Korrektheit einer Gleichung, ob nun theoretisch abgeleitet oder nicht, zu sichern. Der Physiker lernt die Anwendung der DA schon im ersten Semester zu beherrschen. Stellt er in einem höheren Semester eine Gleichung auf, die bei Anwendung der DA nicht korrekt ist, wäre das ein Grund zur Exmatrikulation (was man aber bei der geringen Zahl von Physikstudenten nicht tun wird). Dagegen fällt es Ökonomen in der Regel schwer, auch nur die Wichtigkeit der Angabe von Maßeinheiten einzusehen.

Deshalb ist es verdienstvoll, wenn Fröhlich und Richter sich für die Anwendung der DA einsetzen. Sie gehen noch einen Schritt weiter und fächern sie in 4 Regeln auf, die zu beachten wären. Aus eigener Erfahrung darf ich sagen: Der Physiker kennt im Allgemeinen nur die Regel 1 und diese auch in etwas allgemeinerer Form. Sie lautet schlicht und einfach so wie schon oben formuliert: Jede mathematische Gleichung muss homogen bezüglich der Maßeinheiten der in sie eingehenden Größen sein.

Die Anwendung der DA erfordert etwas Übung und ist zum Teil eine Sache des mathematischen Verständnisses. Man muss beispielsweise wissen, wie eine Taylorreihe richtig notiert wird, und dass log(a) + log(b) = log(ab). Schon aus dieser primitiven Formel ergibt sich, dass man den Logarithmus von Größen unterschiedlicher Dimension durchaus addieren kann. Ein Beispiel wäre die Cobb-Douglas-Produktionsfunktion:

y = A L^αK^β,

die in die logarithmische Gleichung

log y = a + α logL + β logK + ε

umgeformt werden kann (Intriligator 1978: 266 f.). Ökonometriker verwenden diese Gleichung seit Jahrzehnten, und sie ist auch hinsichtlich der Maßeinheiten korrekt, obwohl Y, L und K keine dimensionslosen Größen sind. Es ist falsch, wenn Fröhlich und Richter in ihrer Regel 4 fordern, dass Exponenten und Argumente transzendentaler Funktionen dimensionslose Größen sein müssen. Hier zeigt sich, dass sie die DA selber nicht ganz verstanden haben. Im vorliegenden Fall ist es so, dass Exponenten, Argumente und Parameter derart dimensioniert sind, dass die rechte und die linke Seite hinsichtlich der Dimensionen übereinstimmen.

Vermutlich sind die Autoren in diesem Punkt auf eine Praxis hereingefallen, die bei konsequenter Beachtung der DA korrigiert werden müsste, nämlich dass Elastizitäten, die bekanntlich nicht von den Maßeinheiten der Basisgrößen abhängen, oft als „dimensionslos“ verstanden werden. Streng genommen gibt es aber in einer empirischen Wissenschaft keine dimensionslosen Größen: Auch wenn sich Maßeinheiten formal wegkürzen, ist die übrig bleibende Zahl Ausdruck eines bestimmten Verhältnisses, dem implizit eine Maßeinheit oder eine Kombination von Maßeinheiten zugeordnet ist, die dann meistens neben der Formel – als Hinweis auf ihren Gültigkeitsbereich – notiert wird. Hier zeigt sich noch einmal, dass sich die DA nicht auf die Beachtung der Maßeinheiten beschränkt, die innerhalb einer Formel auftreten.

Fröhlich und Richter demonstrieren außerdem die Wichtigkeit der DA, indem sie den formalen Test der Kontrolle von Maßeinheiten bei der Lösung eines Problems anwenden wollen, für das sich heutzutage leider nur noch wenige Ökonomen interessieren: Der Vergleich der empirischen Warenpreise verschiedener Branchen bzw. Sektoren mit den Werten dieser Waren, die sich aufgrund der neoricardianischen Preisgleichungen bei einer Profitrate von null theoretisch bestimmen lassen. Die Autoren tun das in dem unter den verbliebenen Werttheoretikern ziemlich weit verbreiteten Glauben, jene „direkten Preise“ des von Piero Sraffa (1967) begründeten Modells hätten etwas mit den objektiven Werten der Klassiker der politischen Ökonomie zu tun. Hier das Problem der Autoren: In der werttheoretisch orientierten Literatur gibt es den Streit, ob die gefundenen Korrelationen zwischen Werten und Preisen von den Mengenverhältnissen abhängen oder nicht.

Das ist natürlich eine prachtvolle Gelegenheit, die Nützlichkeit der DA zu demonstrieren, so scheint es jedenfalls. Fröhlich und Richter stellen eine Regressionsgleichung auf, die ihrer Meinung nach DA-mäßig korrekt ist:

(Gleichung 5)

Dabei bedeuten p_i den Preis des Gutes i, x_i die Menge des Gutes i, und d_i ist ein Proxy für den Wert des Gutes i im Sinne der objektiven Wertlehre – Analoges gilt für das Gut j. Dem stellen die Autoren zwei formal identische Gleichungen gegenüber (7+8, hier nur 8 berichtet), die von Díaz und Osuna (2007) verwendet werden und die zeigen sollen, dass die Korrelation zwischen Werten und Preisen von den Mengenverhältnissen abhängen:

(Gleichung 8)

Die Anwendung der DA durch Fröhlich und Richter (2018: 85) ergibt, dass die Gleichung (8) nicht korrekt sein kann. Angeblich verletzt sie die oben bereits erörterte Regel 4. Da diese Regel aber falsch ist, fehlt dieser Kritik an Díaz und Osuna die Begründung.

Es gibt aber ein völlig anderes Problem, an das offenbar keiner der Autoren gedacht hat. Der inhaltliche Fehler solcher Versuche der Überprüfung der klassischen Werttheorie besteht darin, dass in den gängigen Modellen in allen Sektoren „einfache Arbeit“ unterstellt wird (Fröhlich, Richter 2018: 85, Gleichung 9). Zwar kann man sich dabei auf Adam Smith und Karl Marx berufen, aber beide verwandten diese Vereinfachung in ihren Schriften nur zu Demonstrationszwecken, also um es ihren Lesern leichter zu machen, den werttheoretischen Ansatz zu verstehen. Keiner von beiden hat jemals behauptet, dass sämtliche Arbeiter in den verschiedenen Unternehmen, Branchen und Sektoren je Zeiteinheit den gleichen Wert schöpfen. Im Gegenteil! Ihre verbalen Aussagen weisen ausdrücklich darauf hin, dass es so etwas wie Kompliziertheitsgrade der Arbeit gibt (Marx 1890: 211; Smith 1910: 60, 77, 88 ff.). Empirische Tests, die auf einer falschen Messtheorie – in diesem Fall auf den direkten Preisen des neoricardianischen Modells – aufbauen, haben nur wenig mit den Theorien der Klassiker zu tun, auch wenn das manche im Interesse der Aufwertung ihres eigenen Modells behaupten. Direkte Preise sind nicht für die Überprüfung der objektiven Wertlehre geeignet.

Doch zurück zur Dimensionsanalyse! Es hat schon seinen Sinn, wenn Physiker im Studium regelrecht darauf trainiert werden, mit der Sprache und dem Handwerkszeug der Mathematik umzugehen. Auch wenn Ökonomie-Studenten die Mathematiklastigkeit ihrer Ausbildung beklagen, so lässt doch die in der Zunft bislang etablierte Fähigkeit zur korrekten Anwendung der Mathematik auf ökonomische Probleme in manchen Fällen sehr zu wünschen übrig. Aktuell zeigt dass die Analyse von Fröhlich und Richter, auch wenn das Anliegen der Autoren begrüßenswert ist.

Literatur:

Díaz, Emilio; Osuna, Rubén (2007): Indeterminacy in price-value correlation measures. In: Empirical Economics, 33(3): 389-399.

Fröhlich, Nils; Richter, Fabian (2018): Measuring price-value deviations in the light of Dimensional Analysis. In: Gischer, Horst; Hartwig, Jochen; Sahin, Bedia: Bewegungsgesetze des Kapitalismus. Marburg: 77-93.

Intriligator, Michael D. (1978): Econometric Models, Techniques and Applications. Amsterdam, Oxford.

Marx, Karl (1890): Das Kapital, Band 1. In: Marx-Engels-Werke, Band 23. Berlin.

Quaas, Georg (2010): Realgrößen und Preisindizes im alten und im neuen VGR-System. URL: http://mpra.ub.uni-muenchen.de/22316/

Smith, Adam (1910): The Wealth of Nations. New York, Toronto. Nachdruck 1991.

Sraffa, Piero (1967): Warenproduktion mittels Waren. Frankfurt a. M.

Nachwort

Wegen der folgenden beiden Aussagen wurde dieser Beitrag von der neuen Redaktion der „Ökonomentsimme“ nicht angenommen: „Dagegen fällt es Ökonomen in der Regel schwer, auch nur die Wichtigkeit der Angabe von Maßeinheiten einzusehen.“
„Es ist falsch, wenn Fröhlich und Richter in ihrer Regel 4 fordern, dass Exponenten und Argumente transzendentaler Funktionen dimensionslose Größen sein müssen. Hier zeigt sich, dass sie die DA selber nicht ganz verstanden haben.“

In Anbetracht der „Schlachten“ (David Iselin), die auf Ökonomenstimme bereits ausgetragen worden sind, und in Kenntnis dessen, wie zwischen Ökonomen im Allgemeinen diskutiert wird, fand ich diese Kritik kleinlich und zog den Beitrag zurück – zumal eine ausführlichere Version hier zu finden ist.